Contents
- 1 Visão Geral de Análise de Sinais Digitais, Filosofia Geral de Análise de Sinais Digitais e integração desta com Reconhecimento de Padrões
- 2 Classificação dos Métodos: Domínios de Valor, Espaço e Freqüência
- 3 Métodos no Domínio do Valor: Aritmética de Imagens, Thresholding, Histogramas
- 4 Métodos no Domínio do Espaço 1: Convolução Simples e Morfologia Matemática
- 5 Métodos no Domíno do Espaço 2: Detecção de Bordas
- 6 Métodos no Domínio do Espaço 3: Segmentação
- 7 Métodos de Extração de Parâmetros e Rotulação de Objetos
Visão Geral de Análise de Sinais Digitais, Filosofia Geral de Análise de Sinais Digitais e integração desta com Reconhecimento de Padrões
Na área da Visão Computacional e do Reconhecimento de Padrões em Imagens e Sinais Digitais, a verdade crua e dolorosa é que não existe um algoritmo de “Visão Computacional” genérico. A interpretação de padrões em imagens é um processo complexo e constituído de muitos passos. A interpretação de Imagens é realizada através de:
- Um conjunto de algoritmos (filtros) para imagens, cuja natureza varia dependendo do que se quer identificar e do tipo de imagem trabalhado.
- Esses algoritmos são encadeados em uma “pipeline de processamento”.
- Serão sempre extremamente específicos para cada tarefa a ser realizada.
- Variação grande. Conjunto de algoritmos a ser utilizado varia:
- De acordo com a tarefa.
- De acordo com as características da imagem.
Classificação dos Métodos: Domínios de Valor, Espaço e Freqüência
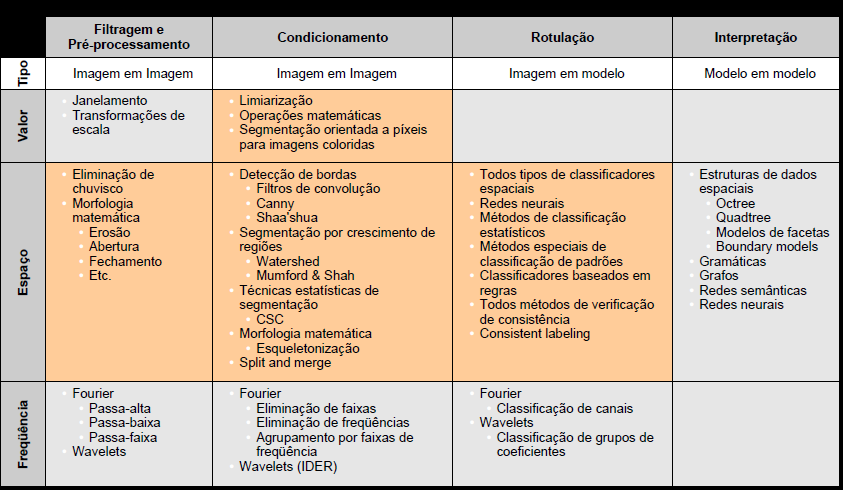
David Marr em seu clássico livro Vision: A Computational Investigation into the Human Representation and Processing of Visual Information, de 1982, lançou as bases para a classificação e sistematização dos métodos de reconhecimento de padrões e análise de imagens, postulando um processo em 4 passos de grau crescente de abstração na análise de uma imagem. Cada passo desse processo seria realizado por um ou mais algoritmos específicos. O ocnjunto de 4 etapas formaria então uma pipeline sequencial, que levaria da imagem sem significado a uma representação simbóilica do que interessa de seu conteúdo. Essas etapas são: (1) Filtragem e Preprocessamento, (2) Condicionamento, (3) Rotulação e (4) Modelagem e Interpretação.
- Filtering and Processing: Não são esperadas modificações profundas nas imagens, elas são apenas atenuadas ou melhoradas.
- Conditioning: Espera-se que uma nova imagem seja gerada e possivelmente ainda a formata.
- Labeling: Início da etapa de interpretação.
- Modeling Interpretation: Classificação e Interpretação dos Dados: Tradução de descrições de estruturas da imagem realizadas anteriormente em linguagens ou esquemas de representação que possuam semântica no contexto de aplicação. Relacionada principalmente com esquemas que levam em consideração aspectos espaciais.
Além disso, podemos “enxergar” uma imagem de três pontos de vista ou “domínios” diferentes: (i) Valor, (ii) Espaço de Imagem e (iii) Freqüencia. Se tomarmos estes 3 possíveis domínios dentro dos quais podemos interpretar os dados de uma imagem; podemos então cruzar estes dois esquemas de classificação e criar a tabela abaixo, que classifica e contextualiza as diversas famílias de algoritmos de processamento de imagens.
A última linha da tabela mostra se se espera uma transformação de uma imagem em outra imagem (I -> I), de uma imagem em uma modelo descritivo ou conjunto de parâmetros descritores (I -> M) ou então se se espera que haja a transformação de um modelo de descrição paramétrica de baixo nível para um modelo mais abstrat (M -> M).
Classificação de Métodos
Métodos no Domínio do Valor: Aritmética de Imagens, Thresholding, Histogramas
V1. Operações Matemáticas de imagem com operando escalarV1.1. Soma: Soma-se um escalar a cada pixel da imagem, aumentando sua intensidade.
V1.2. Multiplicação: Multiplica-se um escalar por cada pixel da imagem. Resultado é expresso em valor inteiro.
Resultados de ambos os métodos são truncados para o valor máximo de representação de pixel no tipo de imagem (no nosso caso 255).
V1.3. Subtração: Subtrai-se um escalar de cada pixel da imagem, reduzindo-se sua intensidade.
V1.4. Divisão inteira: Divide-se o valor de cada pixel da imagem por um escalar. Expressa-se o resultado como inteiro.
Resultados são expressos truncados ao valor mínimo de representação no tipo de imagem (em nosso caso 0).
Implementação: Operações Matemáticas de imagem com operando escalar
- Um único programa implementa todo o conjunto V1.
- Um parâmetro do tipo Símbolo define qual operação será realizada.
Exemplo:
mathescalar -i imagem.pgm -o iresult.pgm -valor 20 -op soma
V2. Operações Lógicas com operando escalar
V2.1. OR: Realiza-se OU lógico entre cada pixel da imagem e operando binário escalar.
V2.2. AND: Realiza-se E lógico entre cada pixel da imagem e operando binário escalar.
V2.3. XOR: Realiza-se OU exclusivo lógico entre cada pixel da imagem e operando binário escalar.
V2.4. NOT: Realiza-se negação lógica de cada pixel da imagem.
Resultados são expressos sempre de forma binária (em nosso caso 0 ou 255)
Implementação:
- Um único programa implementa todo o conjunto V2.
- Um parâmetro do tipo Símbolo define qual operação será realizada.
Exemplo:
boolescalar -i imagem.pgm -o iresult.pgm -valor 1 -op and
V3. Operações Matemáticas de imagem com imagem
V3.1. Soma: Soma-se cada pixel de uma imagem ao correspondente da outra.
V3.2. Multiplicação: Multiplica-se cada pixel de uma imagem com o correspondente da outra. Resultado é expresso em valor inteiro.
Resultados de ambos os métodos são truncados para o valor máximo de representação de pixel no tipo de imagem (no nosso caso 255)
Método só pode ser executado se ambas imagens possuem dimensões iguais (x@y)
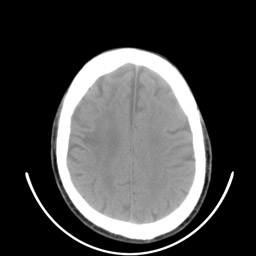
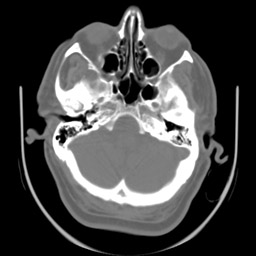
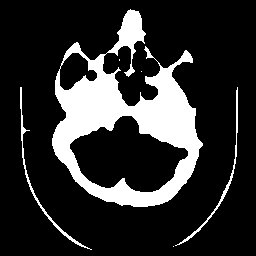
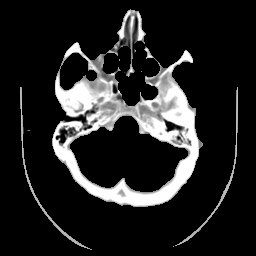
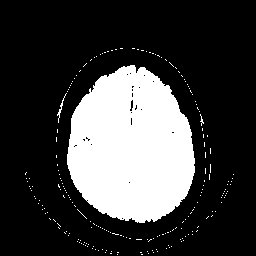
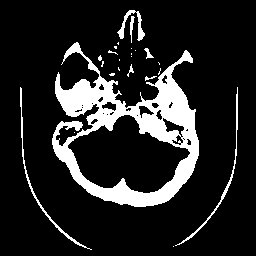
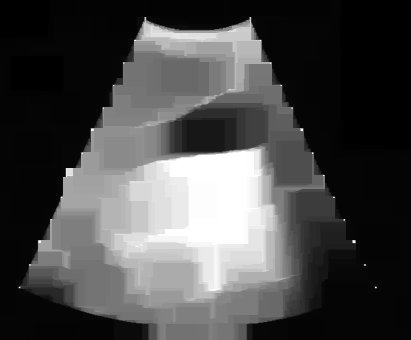
Dois exemplos de aplicação de um operador aritmético entre duas imagens: a máscara binária obtida por limiarização e morfologia matemática a partir da imagem original é multiplicada com esta para a extração do segmento desejado. Observe que no segundo exemplo a máscara continha o artefato em forma de U que foi trazido para a imagem resultante.
| original | máscara | resultado da multiplicação |
 |
 |
 |
 |
 |
 |
V3.3. Subtração: Subtrae-se-se cada pixel de uma imagem do correspondente da outra.
V3.4. Diferença absoluta: Subtrae-se-se cada pixel de uma imagem do correspondente da outra. Resultado é expresso em valor positivo.
V3.5. Divisão: Divide-se cada pixel de uma imagem pelo correspondente da outra. Resultado é expresso em valor inteiro.
Valem as considerações sobre limites mínimos.
- A ordem dos parâmetros de entrada faz diferença.
- Ordem é a mesma da expressão na forma infixada.
Implementação:
- Um único programa implementa todo o conjunto V3.
- Um parâmetro do tipo Símbolo define qual operação será realizada.
Exemplo:
math -i1 imagem.pgm -i2 imagem2.pgm -o iresult.pgm -op dif
V4. Operações Lógicas de imagem com imagem
V4.1. OR: Realiza-se OU lógico entre cada pixel corespondente das imagens.
V4.2. AND: Realiza-se E lógico entre cada pixel corespondente das imagens.
V4.3. XOR: Realiza-se OU exclusivo lógico entre cada pixel corespondente das imagens.
Resultados são expressos sempre de forma binária (em nosso caso 0 ou 255)
- A ordem dos parâmetros de entrada faz diferença.
- Ordem é a mesma da expressão na forma infixada.
Implementação:
- Um único programa implementa todo o conjunto V4.
- Um parâmetro do tipo Símbolo define qual operação será realizada.
Exemplo:
bool -i1 imagem.pgm -i2 imagem2.pgm -o iresult.pgm -op xor
V5. Operações de Limiarização
Limiarização simples
V5.1. Limiar acima: Compara-se cada pixel de uma imagem com um valor limiar. Pixels cujo valor for >= ao limiar recebem a cor #1, o resto a cor #2.
V5.2. Limiar abaixo: Compara-se cada pixel de uma imagem com um valor limiar. Pixels cujo valor for <= ao limiar recebem a cor #1, o resto a cor #2.
Para indicar que as cores são branco e preto, podemos expressar #1 = 255 e #2 = 0. Pode-se perfeitamente definir outros valores.
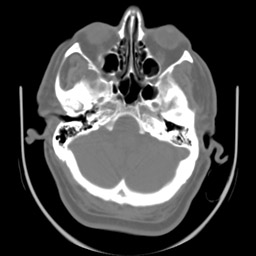
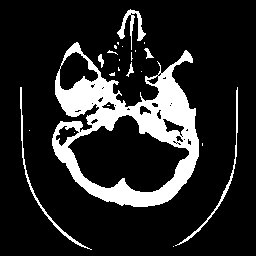
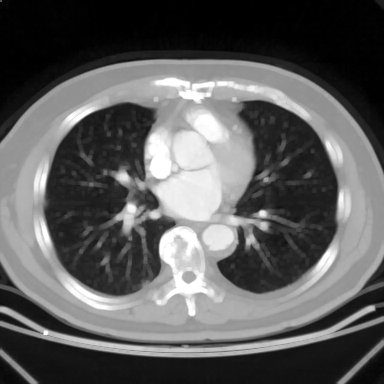
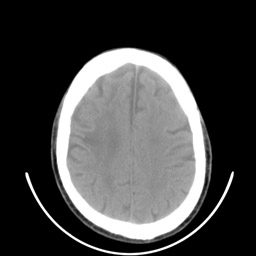
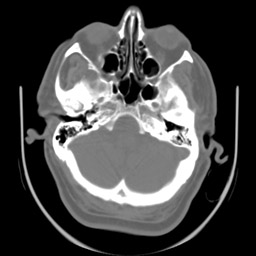
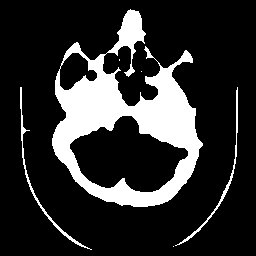
Imagem de tomografia computadorizada de crânio e três diferentes limiarizações. A imagem é de 8 bits e portanto seu valor máximo de pixel é 255. Observe com uma diferença de apenas 5% no limiar, entre 130 e 140 faz uma enorme diferença com relação à quantidade de material indesejável que resulta. O limiarização com valor de 150 será utilizada como máscara em outros exemplos em morfologia matemática.
| image original | limiar de 130 |
 |
 |
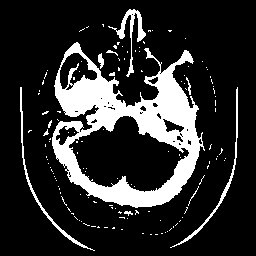| limiar de 140 | limiar de 150 |
 |
 |
Limiarização de faixa
V5.3. Limiar dentro: Compara-se cada pixel de uma imagem com dois valores limiar. Pixels cujo valor for >= ao limiar inferior e <= ao superior recebem a cor #1, o resto a cor #2.
V5.4. Limiar fora: Compara-se cada pixel de uma imagem dois valores limiar. Pixels cujo valor for <= ao limiar inferior e >= ao superior recebem a cor #1, o resto a cor #2.
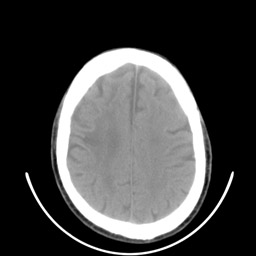
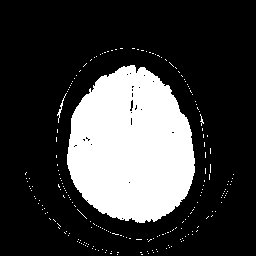
Limiarização com, faixa. Observe que neste caso se obteve um resultado bastante interessante, considerando-se a simplicdade do método, mas não foi posível extrair somente a área de interesse (parênquima cerebral) sem problemas e será necessário um pós processamento com morfologia matemática.
 |
 |
Limiarização com Tolerância
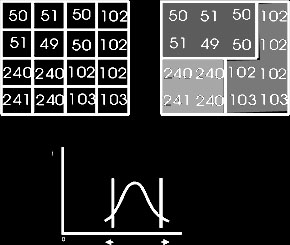
V5.5. Limiar acima com histerese: Compara-se cada pixel de uma imagem com dois valores limiares. Pixels cujo valor for >= ao limiar superior recebem a cor #1, pixels que forem <= ao inferior a cor #2. Pixels entre os limiares são comparados aos seus vizinhos imediatos (vizinhança de 4 ou vizinhança de 8), se algum vizinho estiver acima do limiar, este pixel receberá a cor #1, senão a #2.V5.6. Limiar abaixo com histerese: Compara-se cada pixel de uma imagem com dois valores limiar. Pixels cujo valor for <= ao limiar inferior recebem a cor #1, pixels que forem >= ao superior a cor #2. Pixels entre os limiares são comparados aos seus vizinhos imediatos (vizinhança de 4 ou vizinhança de 8), se algum vizinho estiver abaixo do limiar, este pixel receberá a cor #1, senão a #2.
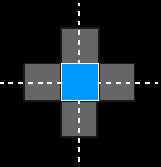
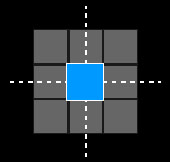
Cálculo de Vizinhança para Operações de Limiarização com Tolerância
| Vizinhança de 4 | Vizinhança de 8 |
 |
 |
Implementação:
- Três programas implementam todo o conjunto V5.
- Limiar Simples
- Limiar com Faixa
- Limiar com Tolerância
- Um parâmetro do tipo Símbolo define qual operação será realizada.
Exemplos:limiarsimples -i imagem.pgm -o iresult.pgm -op acima -lim 100 -c1 255 -c2 0
limiarfaixa -i ima.pgm -o res.pgm -op fora -inf 128 -sup 200 -c1 255 -c2 0
limiartoler -i ima.pgm -o res.pgm -op acima -inf 128 -sup 130 -c1 255 -c2 0
V6. Operações Estatísticas
Para cada possível valor de pixel na escala de valores utilizada (0 a 255 no nosso caso) conta-se o número de pixels apresentando esse valor. Gera-se um vetor contendo esses valores (256 posições no nosso caso) e também uma imagem representando essa contagem como um gráfico de barras.
Implementação do Histograma V6.1:
- Programa toma uma imagem de entrada e gera dois arquivos de saída: a imagem do histograma e o vetor de valores (em ASCII)
Exemplo:
histo -i imagem.pgm -o iresult.pgm -h histo.txt
histo.txt:
255
21 34 56 678 9000 7890 67 5677 456 ....
V6.2. Histograma por Faixas
Calcula-se o histograma dividindo-se a faixa de valores em pedaços dados por seus limites.
Implementação:
- Programa toma uma imagem e um arquivo texto com a definição das faixas de entrada e gera dois arquivos de saída: a imagem do histograma e o vetor de valores (em ASCII)
Exemplo:
histofaixa -i imagem.pgm -f faixas.txt -o result.pgm -h histo.txt
faixas.txt:
4
0 34
35 90
91 200
200 255
V6.3. Pontos Nodais de Histograma
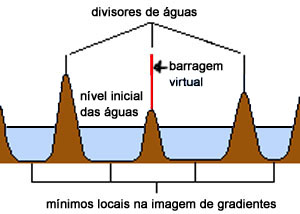
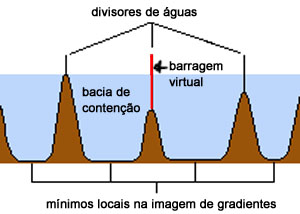
Calcula-se o histograma e procura-se por n fundos-de-vale no mesmo. Gera-se um vetor contendo esses valores.
Implementação do Cálculo de Pontos Nodais em Histograma
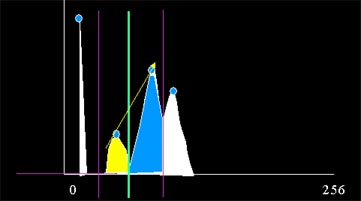
Veja o histograma abaixo. Aparentemente possui dois pontos nodais:
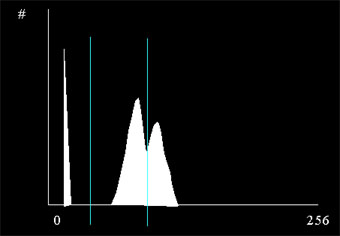
Achando Pontos Nodais em Histograma
- Primeiramente achamos os picos: pontos de valor elevado onde a derivada muda de positivo para negativo. Para evitar que pequenas flutuações incluam erros, sempre tomar um conjunto de valores para o cálculo.
- Depois achamos os vales : pontos pontos entre os picos de menor valor. Se houver uma faixa grande de valor baixo, pegar o meio desta.
Classificando Pontos Nodais em Histograma
- Em terceiro lugar classificamos os vales: vales muito próximos aos picos não nos interessam, pois representam apenas variações de cor de um mesmo grupo.
Verificando Pontos Nodais em Histograma
- Por último calculamos a área (numero de pontos) de cada segmento: segmentos com muito poucos pontos também não nos interessam e são fundidos com o vizinho que possuir tamanho suficiente.
- Exemplo: A área amarela é considerada pequena por que possui poucos pontos e ao mesmo tempo representa um vale relativamente baixo. O ponto nodal em verde claro é eliminado. A área é fundida com a área em laranja, já que esse lado é o da menor amplitude.
Requisitos
- Tolerância no cálculo das derivadas: Usamos uma seqüência de vários valores e uma reta interpolando estes para calcular a derivada tangente. Deve-se implementar o numero de valores como parâmetro.
- Tolerância na identificação do centro de um vale: Ignora-se pequenas variações ao se seguir o fundo de um vale para determinar sua extensão. Implementado como parâmetro.
- Tamanho (área) mínimo de um segmento entre pontos nodais: implementar como parâmetro.
- Seleção de segmentos a fundir: devem ter área abaixo do mínimo e amplitude abaixo de um parâmetro. Melhor forma de expressar isto é multiplicar estes dois valores.
- Número máximo de pontos nodais: parametro definido pelo usuário.
Implementação
Saídas:
- Imagem do histograma mostrando os pontos nodais (mostrar histograma em cinza e pontos nodais como retas verticais em branco).
- Arquivo texto dando lista de valores de pontos nodais.
Linha de comando para forçar encontrar dois pontos nodais:
histonodal -i imagem.pgm -o iresult.pgm -h histo.txt -ntan 10 -tolval 20 -amplitude 50 -area 100 -nodos 2
V7. Operações Combinadas
V7.1. Limiarização com Histograma: Utiliza o resultado de um Cálculo de Pontos Nodais em Histograma para definição dinâmica do limiar. O método de cálculo de pontos nodais é parametrizado para produzir apenas um único ponto nodal. limiarhisto -i imagem.pgm -o iresult.pgm \. .~\z
-op acima -histo histo.txt -c1 255 -c2 0
Métodos no Domínio do Espaço 1: Convolução Simples e Morfologia Matemática
Introdução
Consideramos o valor de cada pixel e também a relação deste com os valores de um conjunto de pixels na sua vizinhança.
- Partes I e II – Operações utilizando Convolução
- Parte III – Operações sobre Regiões
Dividido em três grupos de trabalhos:
E1. Operações Genéricas de Convolução
E2. Morfologia Matemática
E3. Operações de Detecção de Bordas
E1. Operações Genéricas de Convolução
O que é convolução ? Matematicamente, a convolução é uma operação entre duas matrizes, geralmente bidimensionais, uma das quais é a imagem e a outra é um matriz chamada de matriz de convolução ou elemento estruturante.
A matriz de convolução representa uma função matemática qualquer e é aplicada sobre cada pixel g(x,y) da imagem e sua vizinhança imediata, resultando em uma nova imagem gc(x,y), que reflete a relação da imagem original com a função matemática dada pela matriz.
Como realizamos a convolução ? Podemos considerar a convolução como a aplicação de uma máscara de resposta à imagem de acordo com critérios bem definidos. Na convolução temos dois componentes:
- Uma ou mais matrizes de convolução ci(x,y)
- A operação de convolução
A forma mais simples é quando temos apenas uma matriz de convolução e a operação de convolução é a soma dos resultados da multiplicação de cada elemento da matriz com a região da imagem sob a mesma e a subseqüente substituição do valor do pixel sobre o qual a matriz foi aplicada por este resultado.
Exemplo:
|
 |
- Observe que o resultado é sempre escrito na nova imagem resultante
- Observe que se o pixel sob a matriz se encontrar nas bordas da imagem, consideramos apenas os elementos sob a matriz.
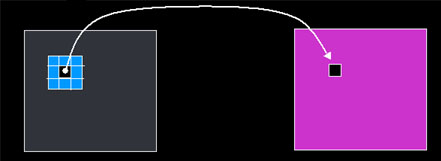
imagem original —> imagem resultante
E1.1 Detecção de pontos salientes
A aplicação de convolução mais simples é a detecção de pontos salientes na imagem. Um ponto saliente é um ponto cujo valor se destaca de seus vizinhos, não necessariamente um valor alto do ponto de vista absoluto.
E1.2 Convolução Genérica
A aplicação de convolução simples pode ser extendida para outros tipos de matriz de filtragem que podem suavizar ou modificar a imagem. É importante possuir-se um programa que leia uma matriz qualquer e aplique o método utilizando:
- Qualquer matriz quadrada de convolução ci(x,y) de dimensões ímpares
- A operação de convolução é sempre a soma das multiplicações das posições correspondentes sob a matriz.
- O pixel de aplicação R é sempre o valor sob o elemento central da matriz
O operador de Laplace é utilizado para a detecção de cruzamentos por zero da Segunda Derivada em uma imagem e não possui direção específica, ao contrário do que veremos nos detectores de bordas de Sobel, Roberts, Robinson e outros, adiante.
Há duas variantes, uma utilizada para consideração de vizinhanças-de-4, h4, e outra para levar em consideração vizinhanças-de-8, h8.
Requisitos para E1.1, E1.2 e E1.3
- Duas entradas: imagem e matriz de convolução
- Ler as duas entradas tanto em P2 como em P5
- Uma saída: Imagem resultante.
E2 – Morfologia Matemática
Morfologia Matemática
- O estudo morfológico concentra-se na estrutura geométrica das imagens.
- Aplica-se morfologia em , realce, filtragem, segmentação, esqueletonização e outras operações afins.
- Definição de uma imagem e feita através de um vetor bidimensional com coordenadas (x, y) para sua representação gráfica .
Conceito de Morfologia Matemática
- Conceito básico: consiste em extrair informações de uma imagem de geometria desconhecida pela transformação com uma outra imagem completamente definida (convolução), chamada elemento estruturante.
- Ao contrário da convolução genérica, na Morfologia Matemática a FORMA do elemento estruturante terá impacto sobre o resultado.
E2.1 Dilatação Binária
A Dilatação expande uma imagem utilizando um Kernel.
Requisitos:
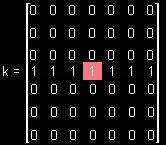
- Usaremos sempre um Kernel quadrado, com Hot Spot no centro da matriz.
- Se quisermos representar um elemento estruturante com forma de linha, faremos uma matriz quadrada, com 1s na linha central e 0s no resto:
Algoritmo informal da dilatação binária:
- Passe o elemento estruturante por todos os pixels da imagem original:
- Se o valor do pixel da imagem sob o elemento central for diferente de zero, copie todos os valores não-zero do elemento estruturante para a imagem resultado.
E2.2. Erosão Binária
A Erosão pode ser definida de forma bem informal como a operação morfológica que encolhe uma imagem de acordo com critérios dados por um elemento estruturante.
Algoritmo informal da erosão binária:
- Passe o elemento estruturante por todos os pixels da imagem original:
- Se nenhum valor dos pixels da imagem sob os valores não-nulos do elemento estruturante for zero, ponha um valor 1 (ou 255) na posição R da imagem resultado.
Existem diversos Operadores e Filtros Morfológicos usando Dilatação/Erosão. Veremos alguns deles adiante.
E2.3 BoundEXT
- Achar todos os pixels que limitam o objeto pelo lado de fora (contorno externo).
- Realiza-se uma dilatação da imagem e desta subtrae-se a imagem original.
E2.4 BoundINT
- Achar o contorno de interno objetos.
- Erode-se a imagem e subtrai-se a imagem erodida da original.
E2.5 Gradiente Morfológico
- Outra forma de encontrar a borda.
- Composta de três outras operações básicas: Dilatação, erosão e a subtração.
- A imagem é dilatada e erodida pelo mesmo kernel e o resultado erodido é subtraído do resultado dilatado. Resulta em uma borda maior e mais confiável.
E2.6 Abertura (Opening)
- Opening – suaviza o contorno de uma imagem.
- Quebra estreitos e elimina proeminências delgadas.
- É usada também para remover ruídos da imagem e abrir pequenos vazios ou espaços entre objetos próximos numa imagem .
- Dada por uma erosão seguida de uma dilatação com o mesmo elemento estruturante.
E2.7 Fechamento
- Closing – Funde pequenos quebras e alargas golfos estreitos. Elimina pequenos orifícios. Irá preencher ou fechar os vazios. Estas operações remover pixels brancos com ruídos.
| 1.imagem original | 3.abertura da imagem limiarizada com kernel branco de 3×3 |
 |
 |
| 2.limiarização por faixa | 4.fechamento com o mesmo kernel de 3×3 |
 |
 |
- A morfologia matemática, como mostra o exemplo acima é muito ítil para a geração de máscaras binárias, utilizadas então em outros tipos de operação, como operações lógicas e operações matemáticas entre imagens. Nem sempre a geração de uma máscara é simples como no exemplo acima. O exemplo abaixo mostra uma máscara gerada através da utilização de um kernel circular de diâmetro 11 pixels.
| imagem original | imagem limiarizada por 150 | fechamento com disco de diâmetro 11 |
 |
 |
 |
Morfologia Matemática – Parte II – Tons de Cinza e Cores
A idéia básica de Morfologia binária extende-se para tom de cinza, mas operações lógicas simulam a conversão aritmética: Uniões se tornam máximos e interseções se tornam mínimos.
E 2.8 Erosão em Tons de Cinza
Algoritmo em Linguagem Informal:
1. Posiciona-se a origem do elemento estruturante sobre o primeiro pixel da imagem que sofre erosão.
2. Calcula-se a diferença de cada par correspondente de valores de pixels do elemento estrutural e da imagem.
3. Acha-se o valor mínimo de todas essas diferenças, e armazena-se o pixel correspondente na imagem de saída para este valor.
4. Repete-se este processo para cada pixel da imagem que sofre erosão.
 |
 |
 |
 |
E 2.8 – Dilatação em Tons de Cinza
Algoritmo em Linguagem Informal:
1. Posiciona-se a origem do elemento estrutural sobre o primeiro pixel da imagem a ser dilatada.
2. Calcula-se a soma de cada par correspondente de valores de pixels do elemento estrutural e da imagem.
3. Acha-se o valor máximo de todas essas somas, e armazena-se o pixel correspondente na imagem de saída para este valor.
4. Repete-se este processo para cada pixel da imagem a ser dilatada.
 |
 |
 |
 |
E 2.10 Fechamento em Tons de Cinza
O fechamento em tons de cinza funciona como o fechamento binário combinando as duas operações de dilatação e erosão em seqüência. A diferença é que a propriedade da idempotência não se aplica: vários fechamentos seguidos produzem uum resultado mais acentuado do que um único fechamento. Isto significa que ium operador do tipo n-fechamento faz sentido. Veremos alguns exemplos adiante.
E 2.11 Abertura em Tons de Cinza
A abertura em tons de cinza funciona como a abertura binária combinando as duas operações de erosão e dilatação em seqüência. A diferença é que a propriedade da idempotência não se aplica: várias aberturas seguidas produzem um resultado mais acentuado do que uma única abertura. Isto significa que ium operador do tipo n-abertura faz sentido. Veremos alguns exemplos adiante.
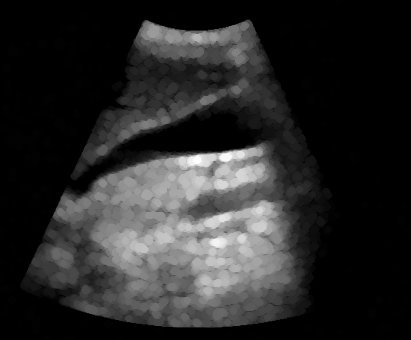
Exemplos de Morfologia Matemática de Tons de Cinza
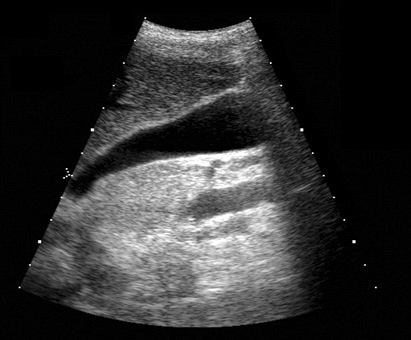
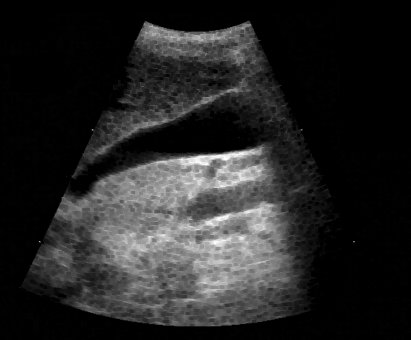
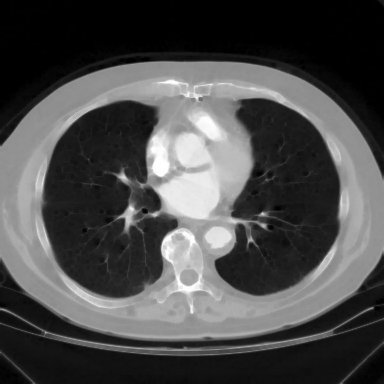
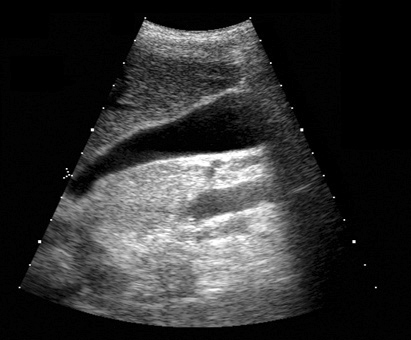
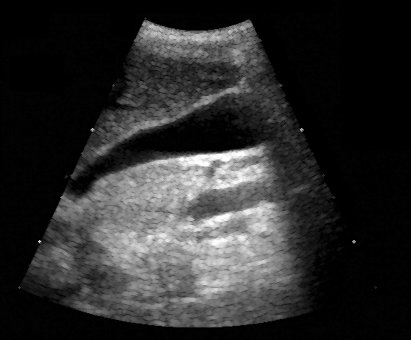
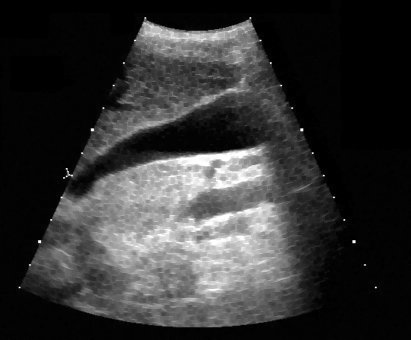
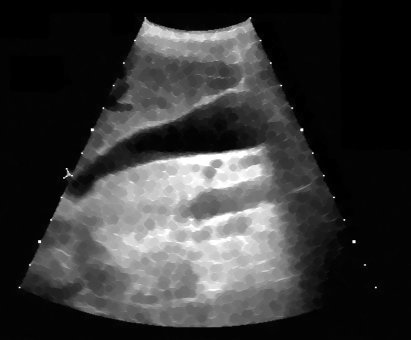
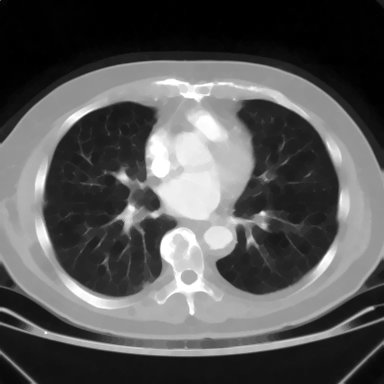
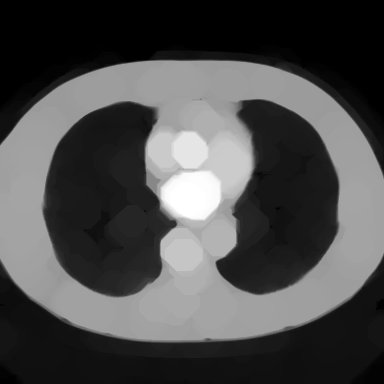
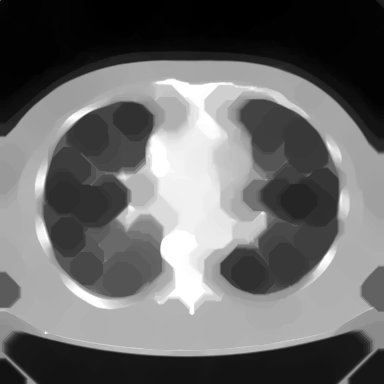
Vários exemplos de aplicação de abertura e fechamento, sempre sobre as imagens originais de ultra-sm e tomografia computadorizada mostradas anteriormente
| aberturas | fechamentos |
| abertura simples com kernel 3×3 | fechamento simples com kernel 3×3 |
 |
 |
| 2 aberturas com disco de diâmetro 7 | 2 fechamentos com disco de diâmetro 7 |
 |
 |
 |
 |
| 5-abertura com disco 7 | 5-fechamento com disco 7 |
 |
 |
| 15-abertura com kernel 3×3 | 15-fechamento com kernel 3×3 |
 |
 |
| 15-abertura com disco 7 da tomografia | 15-fechamento com disco 7 da tomografia |
 |
 |
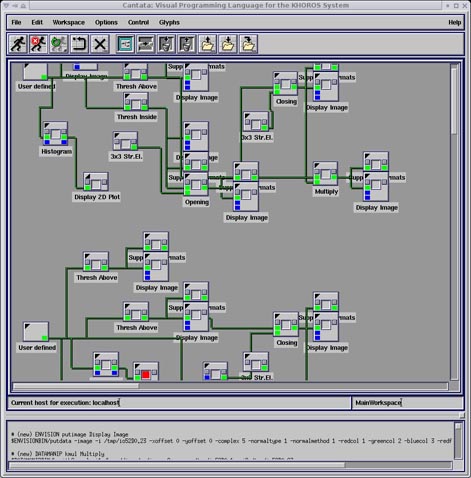
Para você repetir os exemplos acima: Aqui está um workspace para Khoros versão 2.x, contendo em um arquivo as imagens-ponto de partida dessses exemplos e também o workspace para qualquer versão de Khoros 2.0 a 2.2. As imagens fornecidas estão em formato .JPG, lembre-se de convertê-las para PGM ou algo similar antes de usar. Para isso você pode usar o XV, gimp ou outro software livre.
Métodos no Domíno do Espaço 2: Detecção de Bordas
6.6.1. Introdução
Dividido em três grupos de trabalhos que serão implementados pelas equipes.
Borda é o contorno entre um objeto e o fundo indicando o limite entre objetos sobrepostos Um CONTORNO é uma linha fechada formada pelas bordas de um objeto. Mas como conceituamos e detectamos uma borda computacionalmente?
Variações de intensidade complexas que ocorrem em uma região são geralmente chamadas de textura. Bordas são definidas como picos da magnitude do gradiente, ou seja, são variações abruptas que ocorrem ao longo de curvas baseadas nos valores do gradiente da imagem. As bordas são regiões da imagem onde ocorre uma mudança de intensidade em um certo intervalo do espaço, em uma certa direção. Isto corresponde a regiões de alta derivada espacial, que contém alta frequência espacial.
- Borda unidimensional : pode ser definida como uma mudança de uma intensidade baixa para alta. A intensidade do sinal pode ser interferida por ruídos.
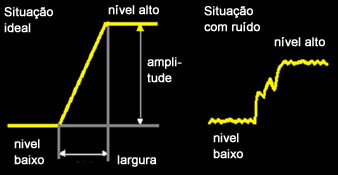Gráfico da intensidade de uma imagem- Borda bidimensional: as descontinuidades ocorrem ao longo de certas linhas ou orientações A orientação é uma característica importante em bordas 2-D
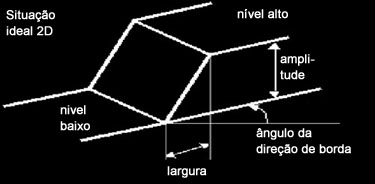Gráfico da intensidade representando uma borda bidimensional.A aquisição da imagem está sujeita a algum tipo de ruído, a situação ideal (sem ruído), na prática não existe. Ruídos não podem ser previstos pois são de natureza randômica e não podem nem mesmo ser medidos precisamente. Porém, algumas vezes ele pode ser caracterizado pelo efeito na imagem, e é geralmente expresso como uma distribuição de probabilidade com uma média específica e um desvio padrão. Existem dois tipos de ruídos específicos:
- Ruído independente do sinal: é um conjunto randômico de níveis de cinza, estatisticamente independente dos dados da imagem. Este tipo de ruído acontece quando a imagem é transmitida eletronicamente de um lugar para outro.
- A – imagem perfeita
- N – é o ruído
- B – imagem final
- B= A+N
- Ruído dependente de sinal: o nível do valor de ruído a cada ponto na imagem é uma função do tom de cinza.
Operadores para detecção de bordas – Operadores de derivadas
Uma vez que uma borda é definida por uma mudança no tom de cinza, quando ocorre uma denscontinuidade na intensidade, ou quando o grandiente da imagem tem uma variação abrupta, um operador que é sensível a estas mudanças operará como um detector de bordas.
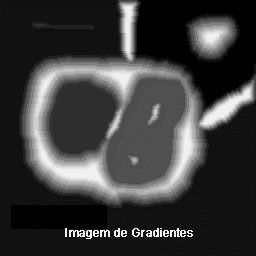
Um operador de derivada faz exatamente esta função. Uma interpretação de uma derivada seria a taxa de mudança de uma função, e a taxa de mudança dos níveis de cinza em uma imagem é maior perto das bordas e menor em áreas constantes. Se pegarmos os valores da intensidade da imagem e acharmos os pontos onde a derivada é um ponto de máximo, nós teremos marcado suas bordas. Dado que as imagens são em duas dimensões, é importante considerar mudanças nos níveis de cinza em muitas direções. Por esta razão, derivadas parciais das imagens são usadas, com as respectivas direções X e Y. Uma estimativa da direção atual da borda pode ser obtida usando as derivadas x e y como os componentes da direção ao longo dos eixos, e computar o vetor soma. O operador envolvido é o gradiente, e se a imagem é vista como uma função de duas variáveis A(x,y) então o gradiente é definido como:
6.6.2. Grupo E3 – Detecção de Bordas com Convolução Simples
E3.1 Roberts
É o mais antigo e simples algoritmos de detecção de bordas. Publicado em L. Roberts Machine Perception of 3-D Solids, Optical and Electro-optical Information Processing, MIT Press 1965. Utiliza uma matriz 2×2 para encontrar as mudanças nas direções x e y.
Máscara ou Kernel de Convolução de Roberts: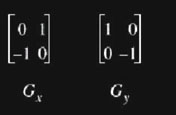 
Para determinar onde o pixel avaliado é ou não um pixel de borda, o gradiente é calculado da seguinte forma:
Fórmula para cálculo do gradiente: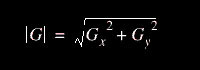 
Se a magnitude calculada é maior do que o menor valor de entrada (definido de acordo com a natureza e qualidade da imagem que esta sendo processada), o pixel é considerado ser parte de um borda. A direção do gradiente da borda, perpendicular a direção da borda, é encontrada com a seguinte fórmula:
Fórmula para cálculo da magnitude: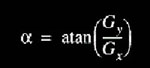 
O pequeno tamanho da máscara para o operador de Roberts torna o mesmo fácil de se implementar e rápido para calcular a máscara de resposta. As
respostas são muito sensíveis ao ruído na imagem.
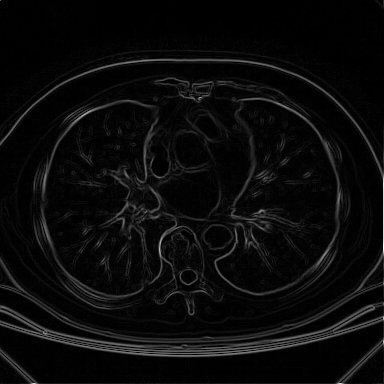
Resultado da aplicação da implementação do Khoros do operador de Roberts
sobre a imagem de tomografia mostrada anteriormente.
E3.2 Sobel
Utiliza duas máscaras para encontrar os gradientes vertical e horizontal das bordas.
Máscaras de Sobel: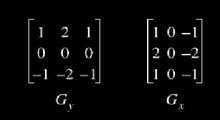 
Considerações sobre o operador de Sobel
- A fórmula para encontrar o gradiente e o ângulo são as similares ao operador de Roberts.
- A computação de |G| se torna mais complexa. Na prática |G| é aproximada da seguinte forma: |G|= |Gx| + |Gy|.
- O ângulo do gradiente corresponde direção de máxima variação da intensidade
- Devido as máscaras serem 3X3 ao invés de 2X2, Sobel é muito menos sensível ao ruído do que Roberts.
- Os resultados são mais precisos e o módulo do gradiente é proporcional a derivada local da intensidade.
- Alguns autores incluem uma terceira matriz para encontra gradientes diagonais, mostrada abaixo. Netse caso temos três e não duas matrizes para o cálculo dos gradientes.
- Alguns autores trabalham com mais três matrizes, que são as negações das três vistas até o momento. Isto permite que se identifique não só a direção mas também o sentido do crescimento do gradiente. Pode ser útil.
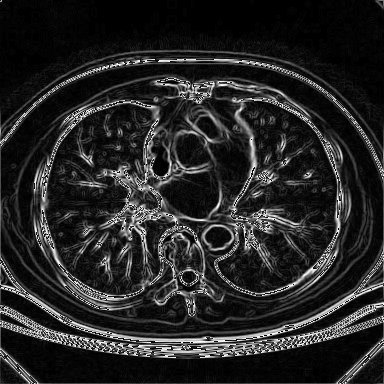
Resultado da aplicação da implementação do Khoros do operador de Sobel
sobre a imagem de tomografia mostrada anteriormente.
E3.3 Robinson
É similar em operação ao de Sobel, porém usa um conjunto de oito máscaras, onde quatro delas são as seguintes:
As outras quatro são simplesmente negações destas quatro.
A magnitude do gradiente é o valor máximo obtido ao aplicar todas as oito máscaras ao pixel vizinho, e o ângulo do gradiente pode ser aproximado como o ângulo na linha de zeros na máscara dando a resposta máxima. Abaixo as quatro matrizes acima com seus respectivos ângulos de preferência:
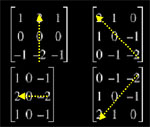
As matrizes negadas possuem mesma direção, mas sentido oposto como ângulo preferencial.
Este algoritmo aumenta a precisão de |G|, mas requer mais computação do que as versões tradicionais de Roberts e Sobel, devido à quantidade de máscaras.
E3.4 Prewitt
O operador de Prewitt é muito similar à versão de 6 matrizes do Operador de Sobel. O que varia é apenas o conjunto de valores das matrizes de convolução, que são definidas como segue:
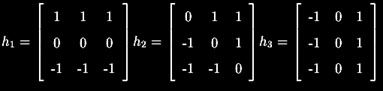
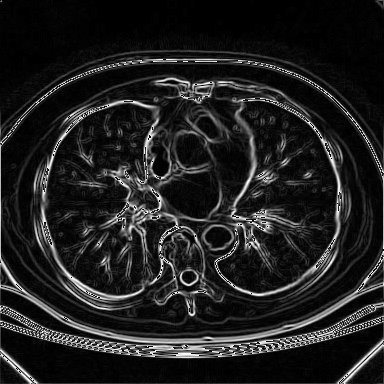
Resultado da aplicação da implementação do Khoros do operador de Prewitt
sobre a imagem de tomografia mostrada anteriormente.
E3.5 Isotrópico
Um operador isotrópico em análise de imagens é um operador que responde de forma igual a variações de intensidade em toda e qualquer direção em uma imagem, sem qualquer preferência por uma direção ou conjunto de direções específico. Um exemplo típico é o detector de cruzamento por zero que responde de forma igual a bordas (na verdade a gradientes) em quaisquer direções. A utilização de suavização gaussiana também atua dessa forma. Na pratica costuma-se utilizar cruzamentos por zero associados a uma suavização gaussiana prévia da imagem. O operador para encontrar cruzamento spor zer pode ser o Laplaciano descrito anteriormente.
No exemplo abaixo não sabemos qual matriz de convolução foi utilizada pois a documenttação do Khoros não menciona e não tentamos fazer negenharia reversa no código-fonte para descobrir. Fica apenas como exemplo. Este operador não vamos implementar.
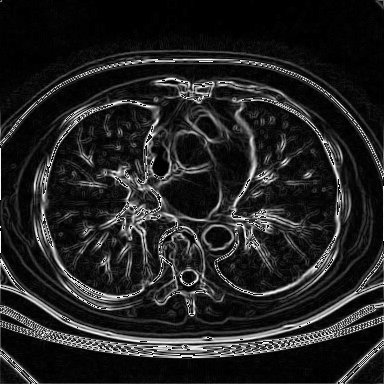
Resultado da aplicação da implementação do Khoros do operador isotrópico
sobre a imagem de tomografia mostrada anteriormente.
6.6.3. Grupo E3’ – Operadores Avançados de Detecção de Bordas
E 3.4 Canny
6.6.4. Grupo E3’’ – Detecção de Estruturas Salientes
E 3.5 Sha’aShua
Links de Detecção de Bordas Mundo Afora
|
. . . 
| Momentos The moment of order (p+q) of a discrete function f(x,y) is defined at the right. The summation is over a domain that includes all nonzero values of the function.We will assume that f(x,y) is a non-negative function with finite values on a bounded image plane. This is appropriate for most image applicationsO Programa Meshgrid fornecido com os algoritmos de cálculo is used to generate the X and Y arrays for the moment calculation. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Massa e Área The total mass of the function is given by the moment m00. When the function has been normalized so that it has unit mass it is sometimes called a probability function.Observe o seguinte: f(x,y) é o “peso” de cada elemento discreto na imagem (pixel). Você pode fazer isso de duas formas diferentes:
|
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Centróide The centroid of f(x,y) is the point at which it will balance. The coordinates of the centroid are found as shown at the right. Note that the function is normalized by dividing by the mass. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Momentos Centrais The central moment is obtained by shifting the origin to the centroid of the function. |
  |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Momentos Centrais Normalizados The normalized central moment of order (p+q) is obtained by dividing the central moment of the same order by a normalization factor. The factor is a function of p and q. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
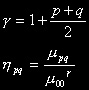| Momentos InvariantesA set of seven invariant moments can be defined by combining the normalized central moments.
The table at the right is from the text, Gonzalez and Woods, page 516, which is based on the paper by Hu (1962). Como eu calculo os etapq‘s ? Fácil: estão representando os momentos centrais normalizados, que são calculados a partir dos momentos centrais, os quais são por sua vez calculados a partir dos momentos de diversas ordens utilizados para compor os momentos invariantes. Basta olhar a fórmula para cálculo do momento acima. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
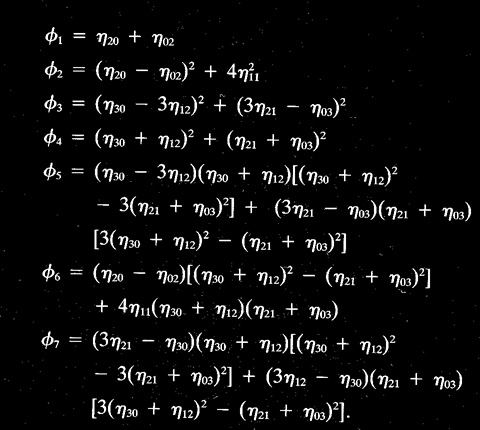Exemplo dos 2 Primeiros Momentos Invariantes phi1 e phi2 aplicados a um Retângulo.
|
Observe os valores de phi1 e phi2 para o mesmo objeto em diversas escalas de magnificação: eles se mantém muiot similares, apresentando invariância de escala. Isto é importante para se poder definir os atributos de um tipo de objeto.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Exemplo dos 4 Primeiros Momentos Invariantes phi1 a phi4 aplicados a uma Figura Geométrica mais complexa.
|
Observe os valores de phi1 a phi4 para o mesmo objeto em diversas escalas de magnificação: eles se mantém menos similares do que no exemplo anterior, por exemplo em 90 graus de inclinação, apresentando uma invariância de escala menor. Neste caso é necessária a comparação de mais momentos para que se possa caracterizar a inclinação do objeto com invariância de tamanho, caracterizando uma segunda operação de reconhecimento d epadrões dentro da operação de reconhecimento de objetos em imagens.
|
Além destes, existe ainda a Excentricidade, cuja forma de cálculo pode ser encontrada na página da Cardiff School of Computer Science.
Algoritmos de Extração de Parâmetros
Observe que as rotinas abaixo calculam um vetor ou um escalar para apenas um segmento de imagem ou para uma imagem contendo apenas um segmento como pixel não-nulo. Significa que você vai ter de fazer o seguinte para usálas:
a) segmente a imagem original e use uma rotina de componentes conexas para separar os segmentos
b) aplique o algoritmo escolhido a cada um dos segmentos.
O material está compilado na Página de Rotinas de Cálculo de Momentos e outros Parâmetros desta Disciplina ou então você pode acessar os capítulos um a um:
Uma outra visão desse mesmo tema é dada por Dave Marshall do Geometric Computing and Computer Vision Group da Cardiff School of Computer Science. Abaixo dois links contendo o mesmo material:
Links de Rotulação de Imagens Mundo Afora
a) Componentes Conexas
- Finding the connected components in an image (usado como base para o algoritmo desta página)
- The MathWorks, Inc.: Connected-Component Labeling
- Applet: Connected Components Labeling Experimentation
- HIPR2: Connected Components Labeling
- Fast Connected Components on Images
- Identifying connected components
6.9. Enunciado do Trabalho FinalO trabalho final consistirá na aplicação de tudo o que você desenvolveu até o momento, tanto RP I como RP II. O material e uma descrição do cenário de aplicação se encontram na página da disicplina entitulada Material para o Trabalho Final Aqui você vai desenvolver um sistema de vigilância automatizado que adquire constantemente imagens de uma câmera e as compara com imagens do local vazio (a aquisição “constante” de imagesn vai ser simulada – usaremos apenas os exemplos providos no material do link anterior). Detectando diferenças entre a referência (local vazio) e a imagem atual, determina quais regiões (objetos) provocaram estas diferenças e calcula um conjunto de parâmetros. Daí utiliza estes parâmetros para calcular se este objeto pertence a uma de três classes: ruído provocado pela movimentação da câmera ou sombras de nuvens (ruíido), um ser humano (intruso) ou um dos animais (cachorros) que patrulham o terreno. Caso seja detectada a presença de um intruso um alarme deverá soar.
Para realizar os testes de procesamento de imagem para implementar esse cenário, utilize a interface de programação visual Cyclops Image Filter fornecida acima e as implementações dos algoritmos de processamento de imagem que você e as outras equipes fizeram durante a disciplina. Faça testes com diferentes algoritmos de filtragem, morfologia e segmentação até obter uma pipeline de processamento satisfatória, que separe os objetos “novos” na imagem e depois calcule os parâmetros descritores destes objetos, escolhendo algoritmos de descrição de objetos dentre os acima que achar adequados. Para a classificação, implemente e utilize um classificador de padrões de sua escolha, como IBL, Rede Neural ou outro.
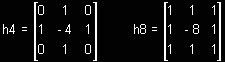
Thiago Rateke is a Computer Vision Researcher with experience mainly focusing on visual perception for autonomous navigation. Finished his PhD degree at Federal University of Santa Catarina (UFSC) in 2020 with focuses on visual perception for Autonomous Navigation. Using approaches like: Stereo Vision, Optical Flow and Convolutional Neural Networks.