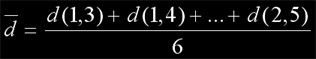Análise de Agrupamentos

Contents

1 Análise de Agrupamentos

Análise de Agrupamentos

O termo Análise de Agrupamentos, primeiramente usado por (Tyron, 1939) na realidade comporta uma variedade de algoritmos de classificação diferentes, todos voltados para uma questão importante em várias áreas da pesquisa: Como organizar dados observados em estruturas que façam sentido, ou como desenvolver taxonomias capazes de classificar dados observados em diferentes classes. Importnate é considerar inclusive, que essas classes devem ser classes que ocorrem “naturalemnte” no conjunto de dados.

Biólogos, por exemplo, têm de organizar dados observados em estruturas que “façam sentido”, ou seja, desenvolver taxonomias. Zoologistas confrontados com uma variedade de espécies de um determinado tipo, por exemplo, têm de conseguir classificar os espécimes observados em grupos antes que tenha sido possível descrever-se esses animais em detalhes de formas a se destacar detalhadamente as diferenças entre espécies e subespécies.

A idéia aqui é a de um processo data-driven, ou seja, dirigido pelos dados observados de forma a agrupar esses dados segundo características comuns que ocorram neles.

Este processo deve levar em conta a possibilidade de se realizar inclusive uma organização hierárquica de grupos, onde a cada nível de abstração maior, são também maiores as diferenças entre elementos contidos em cada grupo, da mesma forma que espécies animais do mesmo gênero têm muito em comum entre si, mas espécies animais que possuem apenas o filo ou a ordem em comum possuem pouca similaridade.

Significância Estatística

Observe que as discussões até o momento não mencionaram a questão da significância estatística ou de seu teste. A Análise de Agrupamentos é na verdade uma coleção de diferentes algoritmos que agrupam objetos. O ponto aqui é que, utilizamos métodos de análise de agrupamentos quando não possuímos nenhuma hipótese a priori sobre a estrutura ou comportamento de nosso dados e necessitamos iniciar com alguma coisa. Por que então não deixar um software descobrir quais regularidades são interessantes no conjunto dos dados ? Por causa disso, testes de significância estatística ainda não são apropriados nesta altura do campeonato.

Áreas de Aplicação

Técnicas de agrupamento têm sido aplicadas em uma enorme gama de áreas. (Hartigan 1975) já provê uma visão geral ampla de vários estudos publicados acerca da utilização de técnicas de Análise de Agrupamentos. Na área médica, por exemplo, agrupamento de doenças por sintoma ou curas pode levar a taxonomias muito úteis. Em áreas da psiquiatria, por exemplo, considera-se que o agrupamento de sintomas como paranóia, esquizofrenia e outros é essencial para a terapia adequada. Na arqueologia, por outro lado, também se tem tentado agrupar civilizações ou épocas de civilizações com base em ferramentas de pedra, objetos funerários, etc. De forma geral, toda vez que se faz necessário que se classifique uma “montanha” de dados desconhecidos em pilhas gerenciáveis, se utiliza métodos de agrupamento.

Métodos de Agrupamento

Há dois algoritmos de agrupamento de dados baseados em métodos estatísticos interessantes para efeitos de classificação de padrões. Vamos analisar e discutir cada um dos dois abaixo e vamos, ao final, discutir como utilizar os resultados da aplicação destes métodos para o particionamento de um grupo de dados cujo comportamento intrínseco ainda não conhecemos na confecção de sistemas de reconhecimento de padrões que sejam capazes de automaticamente classificar novas observações em uma das classes “detectadas” por um destes dois métodos.

Unificação ou Agrupamento em Árvore

A agrupamento em árvore (Tree Clustering) tem por objetivo a construção de taxonomias de vários níveis. Ele é considerado um método de agrupamento aglomerativo hierárquico.

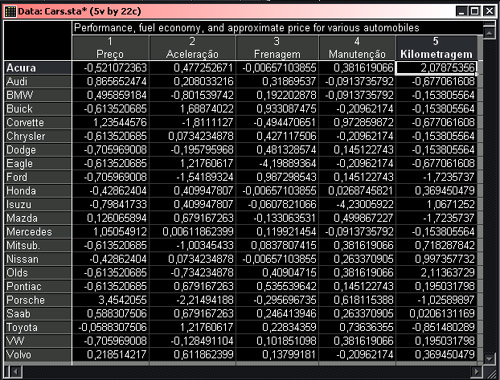
Suponha um conjunto de dados como o abaixo, proveniente do conjunto de exemplos do software Statistica, descrevendo vários carros através de um conjunto de atributos seus. Em quantas classes sensatas podemos dividir este conjunto de carros?

Análise de Agrupamentos

O objetivo deste algoritmo é o de unificar objetos em classes ou grupos sucessivamente maiores através da utilização de alguma medida de similaridade ou de distância. Um resultado típico deste enfoque é uma árvore hierárquica, como no exemplo do dendrograma abaixo:

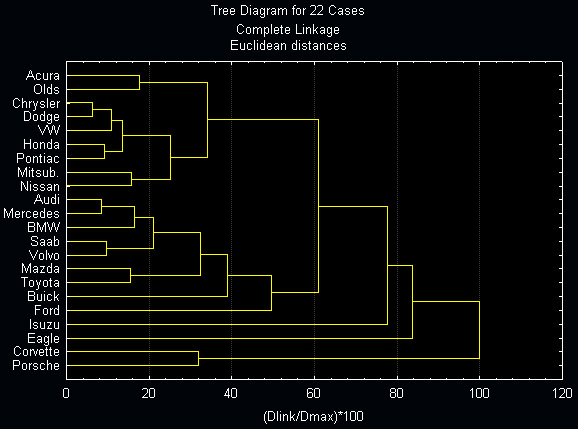
Exemplo de uma árvore hierárquica em uma classificação de tipos de carros de acordo com uma série de características que os descrevem

Para realizar este gráfico acima, o nome de cada instância (não são classes) foi utilizado como variável na posição da variável dependente, neste caso o modelo do carro. As classes são dadas pelos ramos da árvore, que é construída de trás para frente pleo método: começamos ocm ramos individuais e vamos juntando ramos de acordo com a distância (nesse caso euclidiana) entre instâncias, de forma a agrupá-las em classes, até gerarmos a raiz da árvore.

Para construir a árvore utilizamos alguma medida de distância entre classes. Chamamos esta distância de distância de conexão ou linkage distance. Há três filosofias de análise da distância de conexão ao fazer-se a montagem da árvore:

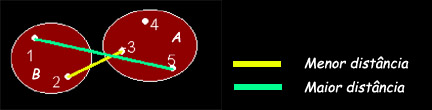
Simples – consideramos a distância entre os vizinhos mais próximos como a distância entre agrupamentos. Neste caso no exemplo abaixo d(A, B) = d(2,3)
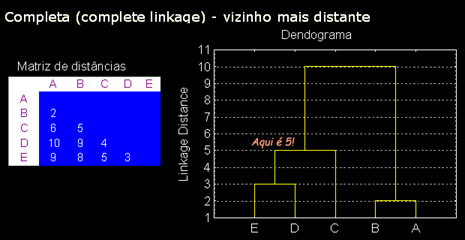
Completa – consideramos a distância entre os vizinhos mais distantes como a distância entre agrupamentos. Neste caso no exemplo abaixo d(A, B) = d(1,5)
Média – Consideramos a distância média segundo a fórmula abaixo como a distância entre agrupamentos.

Distância de Conexão

A fórmula para cálculo da distância média d_média é dada pela média das distâncias entre todos os pares de pontos:

Distância Média

Para montar a árvore de classificação ou dendograma, procedemos unindo sempre grupos apresentando a menor distância de acordo com uma das três regras acima. Veja os exemplos abaixo para esclarecer suas dúvidas:

Dendograma

Para utilizarmos o método para nos dar um determinado conjunto de classes, percorremos a árvore então a partir da raiz, até termos o número de classes que nos agrada mais. No caso acima, por exemplo, se percorrermos a partir da raiz (Dlink/Dmax = 1.0) em direção às folhas e pararmos em Dlink/Dmax = 0.7, teremos 4 classes, dadas cada qual pelo seu ramo correspondente.

Lembre-se que, à medida que você se move para a direita no diagrama de árvore, aumentando as distâncias de conexão, agrupamentos cada vez maiores são formados, com cada vez maiores diversidades intra-agrupamentos. Se este gráfico mostra um platô claro, isto significa que muitos clusters foram formados a aproximadamente a mesma distância de conexão. Esta distância poderia ser um local de corte para a divisão dos dados em grupos ou classes.

Links para Árvores de Decisão e Dendrogramas

Towards Data Science::Decision Tree in Machine Learning (com exemplos em Python)
DENDROGRAM:The Python Graph Gallery
Plotly::Dendrograms in Python
SciPy Hierarchical Clustering and Dendrogram Tutorial

Agrupamento por k-Médias

Este segundo método de Análise de Agrupamentos é um método de agrupamento não-hierárquico por repartição. Este método de agrupamento é muito diferente do método de Agrupamento em Árvore . Suponha que você já tem as hipóteses a respeito do número de conjuntos em seus casos ou variáveis. Você quer informar ao computador para formar exatamente 3 conjuntos que devem ser tão distintos quanto o possível. Este é o tipo de pesquisa que pode ser feita pelo algoritmo de aglomeramento por k-Médias. O método k-Médias produzirá exatamente k diferentes conjuntos com a maior distinção possivel entre eles.

No exemplo dos carros acima, o pesquisador consumidor pode ter um “pressentimento” da experiência de aquisição de carros anteriores ou de análises de mercado que os carros caem basicamente em três categorias diferentes no que diz respeito à relação custo-benefício. Ele pode querer saber se esta intuição pode quantificada, isto é, se a analise de agrupamento por k-Médias das medidas da relação custo-benefício dada pelas variáveis descrityoras dos carros produziria certamente os três conjuntos de narcas de carros como esperados. Assim, as médias das diferentes medidas de relação custo-benefício (frenagem, manutenibilidade, etc) para cada conjunto representariam uma maneira quantitativa de expressar a hipótese ou intuição do pesquisador.

Computacionalmente, você pode pensar neste método como a Análise de Variância (ANOVA) “ao contrário” ; O programa começará com os k-conjuntos aleatórios, e moverá então os objetos entre estes conjuntos com o objetivo de: (1) minimizar o variabilidade dentro dos conjuntos e (2) maximizar o variabilidade entre conjuntos. Isto é semelhante ao “ANOVA , mas ao contrario” no sentido que o teste de significancia ANOVA avalia a variabilidade entre-grupos de encontro a variabilidade intra-grupo ao calcular o teste de significancia para a hipótese em que as medias dos grupos são diferentes para cada grupo. Em k-Médias, as tentativas do programa de mover objetos (por exemplo, casos) dentro e fora dos grupos (conjuntos) para ter resultados ANOVA mais significativos. (porque, entre outros resultados, os resultados ANOVA são a saída padrão da análise de agrupamento).

Para avaliar a precisao da classificação, voce pode comparar a variabilidade intra-grupo ( que é pequena se a classificação é boa) para a variabilidade inter-grupos (que é grande se a classificação é boa). Em outras palavras, voce pode fazer uma analise de variâncias padrão entre-grupos para cada dimensão (caso ou variável). Para um dado k e para cada variável, uma medida de discriminação entre grupos.

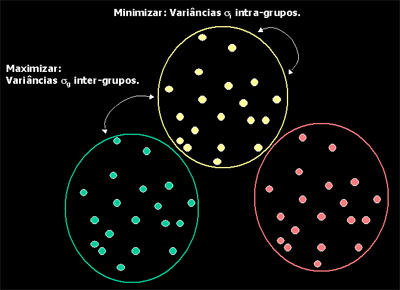
A figura acima ilustra o processo de Análise de Agrupamentos através do método das k-Médias: O processo iterativo é realizado por combinação de elementos em k grupos até que se obtenha uma combinação que maximize o cálulo das variâncias entre grupos e que minimize o cálculo das variâncias intra-grupos

Avaliando a Qualidade de um Agrupamento Gerado

Um agrupamento gerado por este algoritmo é único e o melhor para um dado k, e nenhum mínimo local no processo iterativo é do conhecimento deste autor. Porém, nem todo agrupamento gerado é útil para efeitos de classificação, pois um determinado k, por exemplo k=5, pode refletir um número de classes inadequado para a divisão de uma determinada população de observações. É necessário encontrar o valor de k que melhor reflita a “divisão natural” da população de dados observada. Para avaliar se uma classificação é apropriada, pode-se comparar a variância intracluster (que deverá ser pequena se a divisão em classes for adequada) à variância inter-clusters (que deverá ser grande se a classificação em categorias for boa). Isto significa que uma boa divisão de um conjunto de observações em grupos ou categorias é aquela onde os elementos de uma mesma categoria são o mais parecidos entre si (menor variância intra-cluster) e onde os elementos de grupos diferentes são o mais diferentes entre si possível (variância inter-cluster ou inter-grupos). Isto é dito verificar a robustez dos grupos de objetos ou categorias geradas.

Para tanto, você pode realizar uma análise de variância padrão inter-grupos. Para um dado k e para cada variável, uma medida de discriminação entre grupos pode ser dada pelo cálculo das variâncias inter- e intra-grupos e pelo coeficiente de discriminação F, dado abaixo:

Análise de Variância

Pode-se utilizar F como medida da qualidade de um determinado conjunto de classes como subdivisão natural de um conjunto de dados, quando não se sabe se para determinado conjunto de dados 2,3 ou 4 classes são o mais adequado.
Algoritmo Básico do Método das k-Médias

Padronize ou estandardize todos os dados, descrevendo cada variável em termos de distância de seu valor em desvios-padrão da sua média.
Fixa-se o número de agrupamentos desejado = k;
Divida os casos aleatoriamente nos k grupos;
Calcula-se o centróide de cada grupo;
Com os dados padronizados, calcula-se, para cada caso, a distância euclidiana em relação ao centróide de cada grupo;
Transfira o caso para o grupo cuja distância ao centróide é mínima;
Repita (4), (5) e (6) até que nenhum caso seja mais transferido.

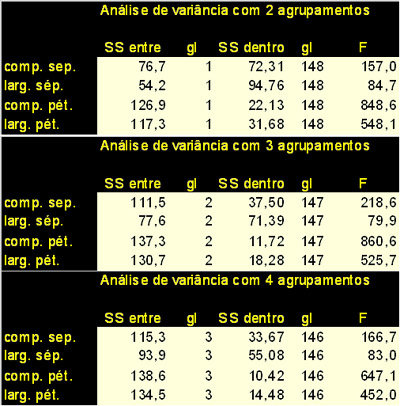
O exemplo do conjunto de dados das flores do gênero Iris utilizado para a Análise de Discriminantes também é um bom exemplo que pode ser utilizado com o algoritmo de k-médias para produzir um conjunto de classes naturais. Ele nos permite uma boa análise das variâncias:

Análise de Variância

Exemplo de Agrupamento por k-Médias

Tome novamente o caso dos modelos de carros, dado acima. A meta do algoritmo k-means é encontrar um particionamento ótimo para dividir um número de objetos em k agrupamentos. Este procedimento irá mover objetos de agrupamento para agrupamento com o objetivo de minimizar a variância intra-grupo e maximizar a variancia entre-grupos. Neste exemplo, você pode identificar 3 agrupamentos nos dados sobre carros, usando o metodo de agrupamento em árvore (Joining) Agora você verá que o tipo de solução fornecida pelo agrupamento por k-medias irá sugerir 3 grupos.

Se executarmos este exemplo no software Statistica, setando “casos” como objetos a agrupar e k=3, obtemos o seguinte relatório, após o término do processamento da análise de agrupamentos:

Number of variables: 5
Number of cases: 22
K-means clustering of cases
Missing data were casewise deleted
Number of clusters: 3
Solution was obtained after 3 iterations

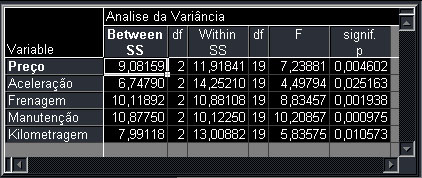
Este processamento nos provê vários conjuntos de valores que vão nos permitir utilizar o resultado para um classificador. A primeira etapa é observar a análise da variância, que para nosso caso é como abaixo:

Análise de Variância

Nesse caso, a julgar pela magnitude e níveis de significância dos valores de F, as variáveis Manutenção, Frenagem e Preço representam os critérios mais importantes para a atribuição de objetos a grupos.

Utilizando o Resultado da Análise de Agrupamentos para Construir um Classificador de Padrões

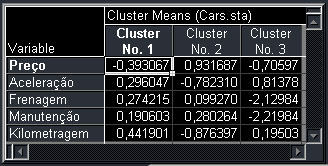
Esse valores acima somente servem para nos permitir avaliar a qualidade dos clusters gerados, são pouco interessantes para um classificador. Já as médias dos valores de cada cluster, que representam uma espécie de centróide de cada cluster:

Cluster Means

Considerando que cada uma destas 3 médias representa um ponto no R⁵, que é o espaço de casos deste conjunto de dados, poderíamos considerar estes valores como uma espécie de protótipos de referência para um classificador. Mas temos também a opção de usar as próprias instâncias de casos e sua respectiva classificação.

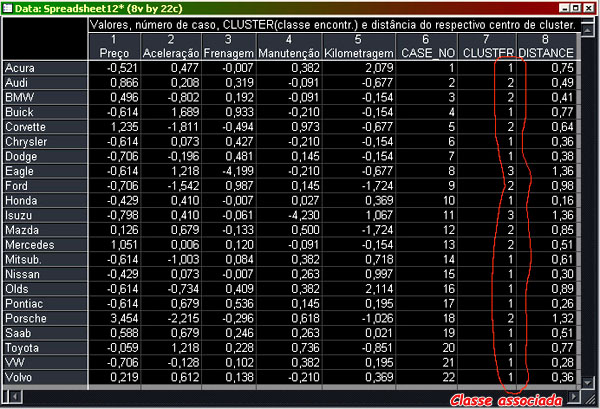
Para saber como foram classificados os casos, pode-se observar a tabela de classificação geral de caso por grupo/classe:

Tabela de Classificação

Para a construção de um classificador de novos casos, é esta tabela que é a mas interessante. Uma opção de uso desses resultados é considerar o cluster associado a cada caso como sendo a classe encontrada para o caso, ou seja, sua classificação e utilizar esta informação em um método de aprendizado supervisionado para criar um classificador para novos casos ou simplesmente utilizar esta lista de casos “classificados”. Este método pode ser uma coisa complexa como uma rede neural ou uma coisa simples como k-NearestNeighbour.

Exercício de Análise de Agrupamentos: Implementação dos dois principais métodos de Análise de Agrupamentos

Implemente os dois métodos de Análise de Agrupamentos vistos acima em um programa de computador, de tal forma que o usuário possa ler um arquivo de dados organizado em colunas divididas por tabs e escolher entre um dos dois métodos. Os requisitos da implementação de cada um dos dois métodos são dados abaixo:

Requisitos da Implementação do Agrupamento em Árvore

O programa deverá permitir ao usuário escolher entre Distância de Hamming e Distância Euclideana como métricas de similaridade.
O programa deverá permitir ao usuário escolher entre as três distâncias de conexão ou linkage distances.
O programa deverá mostrar ao usuário o dendrograma da classificação gerada.
O programa deverá permitir que se exporte o arquivo de dados com a classe atribuída a cada objeto/observação.

Requsitos da Implementação do Agrupamento por k-Médias

O programa deverá permitir ao usuário escolher o valor de k.
O programa deverá permitir ao usuário gerar classificações com vários ks e guardar o resultado de cada uma, de forma que se possa compará-las.
O programa deverá permitir que o usuário opte pelo cálculo dos valores de variância interna e externa e de F para realizar a análise de dados dos resultados produzidos.
O programa deverá permitir que se exporte o arquivo de dados com a classe atribuída a cada objeto/observação.

Links de Análise de Agrupamentos por k-Médias

K-Means Clustering Implementation in Python | Kaggle
K-Means Clustering in Python – Blog by Mubaris NK
K-means Clustering in Python – Ben Alex Keen
K-Means Clustering in Python with scikit-learn – DataCamp
In Depth: k-Means Clustering | Python Data Science Handbook (com sugestões de como realizar agrupamentos usando bordas não-linares)
sklearn.cluster.KMeans — scikit-learn 0.20.0 documentation

Discussões, Toques e Ideias de k-Means para Visão Computacional

Towards Data Science::Extracting colours from an image using k-means clustering (com exemplos de código em JavaScript)

Análise de Agrupamentos